 Gambling
related articles
Gambling
related articles
Modelling Results of AFL Games - Part 3
Introduction
By
Scott McIntosh
"In the run betting" is a popular betting
option offered by bookmakers. In the third and final
part of this series of articles I will describe how
the normal distribution model of AFL game results
can be applied to calculate probabilities during the
course of a game.
Method
Given the amount of time remaining and the current
score difference in a game we can calculate probabilities
of the game result based on the before the game predicted
line and standard deviation. These calculations assume
that the predicted line and standard deviation per
time unit does not vary during the course of a game.
Given:
- line = before the game predicted line
- stdev = before the game standard deviation
- time = proprotion of game remaining (e.g. 1 =
before game, 0.75 = quarter time, 0.5 = half time,
0 = game over)
- score = current score difference
We calculate:
- Adjusted Line = (line * time) + score
- Adjusted Standard Deviation = stdev * square root(time)
Using the adjusted predicted line and standard deviation
the probability of any result occuring can be calculated
as described in Part 2.
Example
Team 1 is a 15.5 point favourite and is behind by
20 points at quarter time. We want to calculate the
probability and fair odds for each team winning the
game.
Adjusted Line = (15.5 * 0.75) + (-20) = -8.375
Adjusted Standard Deviation = 38 * square root(0.75)
= 32.98097
Using Excel as described in Part 2
Probability Team 1 wins = normdist(999, -8.375, 32.98097,
true) - normdist(0.5, -8.375, 32.98097, true) = 0.393702
Fair Odds = 1 / 0.393702 = $2.54
Repeating this procedure for all results we obtain
the table below.
| Winner |
Before Game |
Quarter Time |
| |
Probability |
Fair Odds |
Probability |
Fair Odds |
| Team 1 |
0.653481 |
$1.53 |
0.393702 |
$2.54 |
| Team 2 |
0.336858 |
$2.97 |
0.594562 |
$1.68 |
| Draw |
0.009660 |
$103.52 |
0.011736 |
$85.21 |
Accuracy
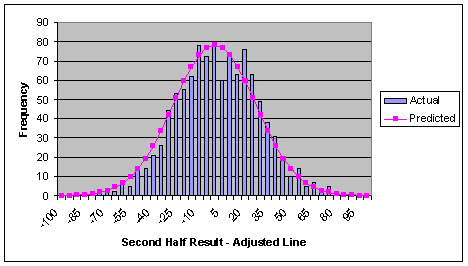
Graph 3 represents how well the normal distribution
model fits time periods smaller than the whole game,
a major assumption for calculating in the run probabilities.
The result (i.e. score difference) for the second
half only was compared to what the model predicted.
The before the game predicted line used is the bookmakers
line and the second half adjusted line is 0.5 times
the bookmakers line. The standard deviation used for
the predicted frequency curve is 26.87006 (38 * square
root(0.5)). From observation there is a close fit
between the actual and predicted results which statistical
tests confirm.
Graph 3: Second Half Results
(1056 Home and Away Games : 2000 - 2005)
Limitations
The major assumption for calculating in the run probabilities
is that the predicted line and standard deviation
do not change over time. Whilst this may be true for
most of the game towards the end of the game this
may not be true. A team winning by a small margin
may "waste time" to increase their winning
chances. This would have the effect of decreasing
the standard deviation and average winning margin.
Another limitation towards the end of the game is
the discrete scoring nature of the game, a goal is
worth six points and a behind 1 point. With time remaining
for 1 scoring shot only there is no difference if
a team is winning by 2, 3, 4 or 5 points although
the model would say there are significant differences.
Conclusion
Despite the relative simplicity of the normal distribution
model and the assumptions that are made, reasonably
accurate estimates of probabilities can be made before
and during the course of an AFL game. More accurate
predictions might be able to be made using more factors
(e.g weather) which would require more data and further
investigation.
Scott
McIntosh runs the website Online
Poker Room Reviews
Article index
Home|FAQs|Disclaimer|Contact
Us
©2000 to present.
OZmium Pty Ltd. All rights reserved